huhuhang大佬
2. 线性回归实现与应用
2.1 介绍
线性回归是一种较为简单，但十分重要的机器学习方法，掌握线性的原理及求解方法，是深入了解线性回归的基本要求。除此之外，线性回归也是监督学习回归部分的基石。
2.2 知识点
- 一元线性回归
- 平方损失函数
- 最小二乘法及代数求解
- 最小二乘法及矩阵求解
- 线性回归综合案例
2.3 线性回归介绍
上一节，我们了解了分类和回归问题的区别。也就是说，回归问题旨在实现对连续值的预测，例如股票的价格、房价的趋势等。如下图，展现了房屋面积和价格对应的关系图。
不同的房屋面积对应这不同的价格，现在，假设我手中有一套房屋想要出售，而出售时就需要预先对房屋进行估值。于是，我想通过上图，也就是其他房屋的售价来判断手中的房屋价值是多少，应该怎么做呢，如下图所示,
首先绘制了一条红色的直线，让其大致验证数据色点分布的延伸趋势。然后，我将已知房屋的面积大小对应到红色直线上，也就是蓝色点所在位置。最后，再找到蓝色点对应于房屋的价格作为房屋最终的预估价值。
在上图呈现的这个过程中，通过找到一条直线去拟合数据点的分布趋势的过程，就是线性回归的过程。而线性回归中的线性代指线性关系，也就是图中绘制的红色直线。
2.4 一元线性回归
上面针对线性回归的介绍内容中，房屋面积为自变量，房价为因变量。我们将只有一个自变量的线性拟合过程叫做一元线性回归。 下面，我们就生成一组房屋面积和房价变化的示例数据。x为房屋面积，单位是平方米；y为房价，单位是万元。
import warnings
# 减少代码执行过程中不必要的错误提示
warnings.filterwarnings("ignore")
import numpyas np
from matplotlib import pyplot as plt
x = np.array([56, 72, 69, 88, 102, 86, 76, 79, 94, 74])
y = np.array([92, 102, 86, 110, 130, 99, 96, 102, 105, 92])
plt.scatter(x, y)
plt.xlabel("Area")
plt.ylabel("Price")
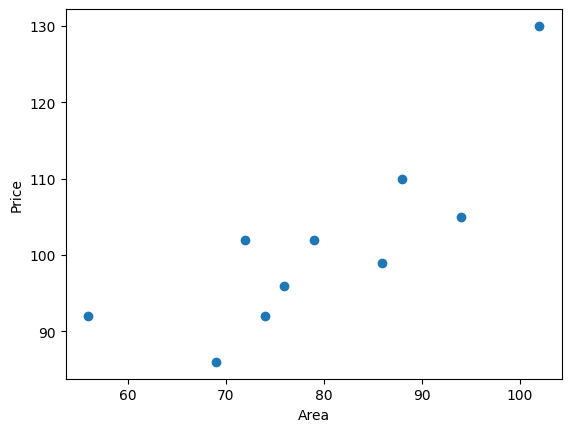线性回归即通过线性方程去拟合数据点。那么，我们可以令该一次函数表达式为：y(x,w) = w0+w1x
接下来，我们对公式进行代码实现。
def f(x: list, w0: float, w1: float):
"""一元一次函数表达式"""
y = w0 + w1 * x
return y
那么，那一条直线最能反应出数据的变化趋势呢？想要找出对数据集拟合效果最好的直线，这里再拿出下图，如下图所示，当我们使用y(x,w) = w0+w1x对数据进行拟合时，就能得到拟合的整体误差，即图中蓝色线段的长度总和。如果某一条直线对应的误差值最小，是不是就代表这条直线最能反映数据点的分布趋势呢？
2.5 平方损失函数
正如上面所说，如果一个数据点为（xi,yi）,那么他对应的误差就为yi-(w0+w1xi)。上面的误差往往也称之为残差。但是在机器学习中，我们更喜欢称作损失，即真实值和预测值之间的偏离程度。那么，对n个全部数据点而言，其对应的残差损失总和就为： 所有点的残差总和，更进一步，在线性回归中，我们一般使用残差的平方和表示所有样本点的误差。这样能保证损失始终是累加的正数，而不会存在正负残差抵消的问题，这与这个总和，机器学习中有一个专门的名词，那就是平方损失函数。而为了得到拟合参数w0和w1最优的数值，我们的目标就是让其对应的平方损失函数最小。
def square_loss(x: np.ndarray, y: np.ndarray, w0: float, w1: float):
"""平方损失函数"""
loss = sum(np.square(y - (w0 + w1 * x)))
return loss
如果某条直线拟合样本得到的总损失最小，那么这条直线就是最终想得到的结果，而求解损失最小值的过程，就必须用到下面的数学方法了（最小二乘法）。
2.6 最小二乘法代数求解
最小二乘法是用于求解线性回归拟合参数$$w$$的一种常用方法。最小二乘法中的二乘代表平方，最小二乘也就是最小平方。而这里的平方就是指代上面的平方损失函数。 简单来讲，最小二乘法也就是求解平方损失函数最小值的方法。那么，到底该怎样求解呢？这就需要使用到高等数学中的知识。推导如下： 首先，平方损失函数为： $$f = \sum__{i=1}^N {(y_{i}-(w_0 + w_1x_{i}))^2}$$
我们的目标是求取平方损失函数$$min(f)$$最小时，对应的$$w$$。首先求$$f$$的1阶偏导数：
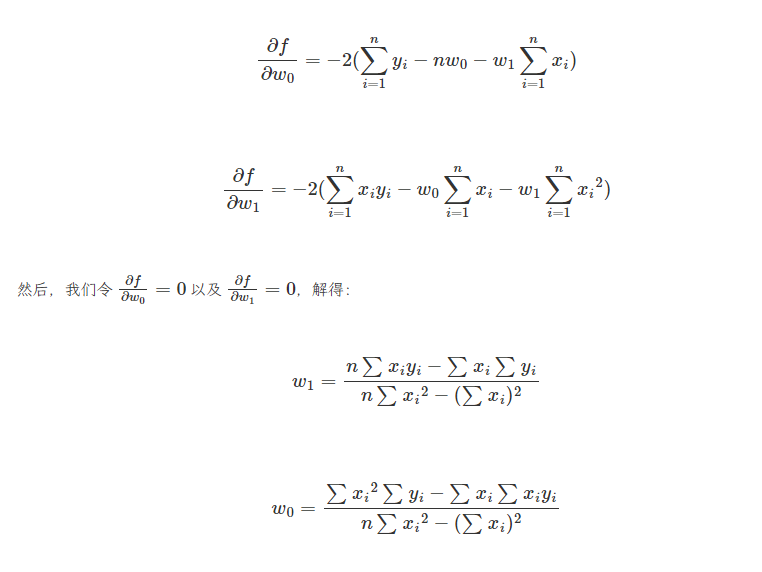到目前为止，已经求出了平方损失函数最小时对应的$$w$$参数值，这也就是最佳拟合直线。我们将公式求解得到$$w$$
的过程进行代码实现：
def least_squares_algebraic(x: np.ndarray, y: np.ndarray):
"""最小二乘法代数求解"""
n = x.shape[0]
w1 = (n * sum(x * y) - sum(x) * sum(y)) / (n * sum(x * x) - sum(x) * sum(x))
w0 = (sum(x * x) * sum(y) - sum(x) * sum(x * y)) / (
n * sum(x * x) - sum(x) * sum(x)
)
return w0, w1
于是，可以向函数least_suqres_algebraic(x,y)传入$$x$$和$$y$$得到$$w0$$和$$w1$$的值。然后带入求得的$$w0$$和$$w1$$到square_loss(x,y,w0,w1)可以得到对应的平方损失的值，接下来，我们尝试将拟合得到的直线绘制到原图中：
x_temp = np.linspace(50, 120, 100) # 绘制直线生成的临时点
plt.scatter(x, y)
plt.plot(x_temp, x_temp * w1 + w0, "r")
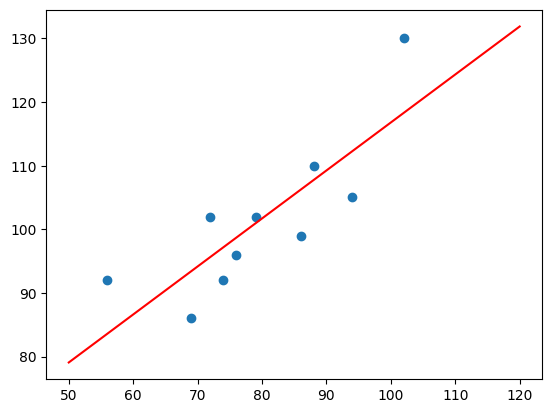
从上图可以看出，拟合的效果时不错的。那么，你就可以对应你手中房屋的面积获得一个预估的价格，只需带入方程即可求解。
2.7 最小二乘法矩阵求解
学习玩上面的内容，即可了解什么时最小二乘法，以及如何使用最小二乘法进行线性回归拟合。上面，我们采用了求偏导数的方法，并通过代数求解找到了最佳拟合参数$$w$$的值。这里尝试另外一种方法，即通过矩阵的变换来计算参数$$w$$。
首先，一元线性函数的表达式为$$y(x,w)=w_0+w_1x$$,表达成矩阵的形式为：
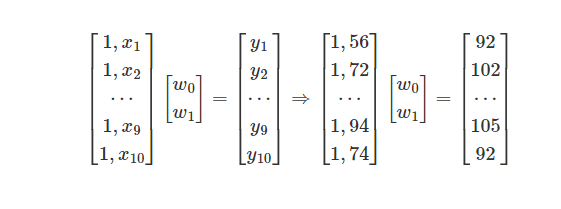
即：
$$y(x,w)=XW$$
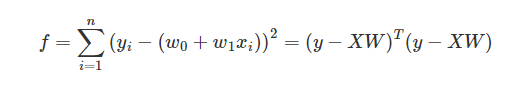
由矩阵乘法分配律得到：
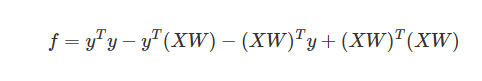
在该公式中$$y$$与$$XW$$皆为相同形式的$$(m,1)$$矩阵，由此两者相乘属于线性关系，所以等价转换如下：
此时，对矩阵求偏导数得到：
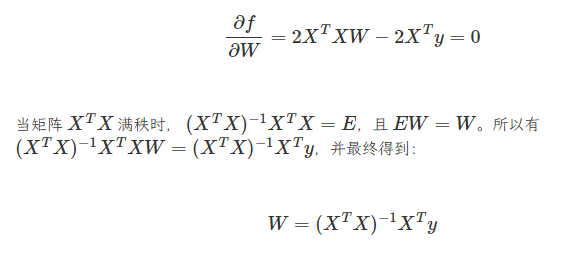我们可以由代码实现：
def least_squares_matrix(x: np.matrix, y: np.matrix):
"""最小二乘法矩阵求解"""
w = (x.T * x).I * x.T * y
return w
计算时，需要参考上方计算公式对原$$x$$数据添加截距项系数1，这里使用np.hastack方法。
x_matrix = np.matrix(np.hstack((np.ones((x.shape[0], 1)), x.reshape(x.shape[0], 1))))
y_matrix = np.matrix(y.reshape(y.shape[0], 1))
x_matrix, y_matrix
使用矩阵计算的优点在于，当我们面对千万或上亿级规模的数据时，矩阵的计算效率就会高出很多。这就是为什么要学习矩阵计算的原因。
2.8 线性回归scikit-learn实现
上面的内容中，我们学习了什么时最小二乘法，以及使用python对最小二乘线性回归进行了完整实现。那么，我们如何利用机器学习开源模块scikit-learn实现最小二乘线性回归方法呢？使用scikit-learn实现线性回归过程会简单很多，这里要用到LinearRegression()类。看一下其中的参数
sklearn.linear_model.LinearRegression(fit_intercept=True, normalize=False, copy_X=True, n_jobs=1)
- fit_intercept: 默认为 True，计算截距项。
- normalize: 默认为 False，不针对数据进行标准化处理。
- copy_X: 默认为 True，即使用数据的副本进行操作，防止影响原数据。
- n_jobs: 计算时的作业数量。默认为 1，若为 -1 则使用全部 CPU 参与运算。
from sklearn.linear_model import LinearRegression
# 定义线性回归模型
model = LinearRegression()
model.fit(x.reshape(x.shape[0],1),y) # 训练，reshape操作把数据处理成fit能接受的shape
# 得到模型拟合参数
model.intercept_,model.coef_
这里，通过model.intercept_可以得到拟合的截距项，即上面的$$w_0$$，通过model.coef_得到$$x$$的系数，即上面的$$w_1$$。对比发现，结果完全一致。同样我们输入面积150平方进行预测价格：
model.predict([[150]])
运行上面这段代码可以得到array([154.52273298])，这样的输出。与自行实现计算结果一致。
2.9 线性回归综合案例
目前，我们已经掌握了如何使用最小二乘法进行线性回归拟合，以及通过代数计算矩阵变换两种方式计算拟合系数$$w$$,这已经达到了掌握线性回归方法的要求。接下来，我们将尝试加载一个真实数据集，并使用scikit-learn构建预测模型，并实现回归预测。 这里我们采用一个真实的房价数据集，波士顿房价数据集。
2.9.1 数据集介绍及划分
波士顿房价数据集是机器学习中分厂经典的数据集，它被用于多篇回归算法研究的学术论文中。该数据集共计506条，其中包含13个与房价相关的特征以及1个目标值（房价）。首先，我们使用Pandas加载并预估数据集，同时查看DataFrame前5行数据。
import pandas as pd
df = pd.read_csv('https://cdn.huhuhang.com/hands-on-ai/files/course-5-boston.csv')
df.head()
该数据集统计了波士顿地区各城镇的住房价格中位数，以及与之相关的特征。每列数据的列名解释如下：
- CRIM: 城镇犯罪率。
- ZN: 占地面积超过 2.5 万平方英尺的住宅用地比例。
- INDUS: 城镇非零售业务地区的比例。
- CHAS: 查尔斯河是否经过 (=1 经过，=0 不经过)。
- NOX: 一氧化氮浓度（每 1000 万份）。
- RM: 住宅平均房间数。
- AGE: 所有者年龄。
- DIS: 与就业中心的距离。
- RAD: 公路可达性指数。
- TAX: 物业税率。
- PTRATIO: 城镇师生比例。
- BLACK: 城镇的黑人指数。
- LSTAT: 人口中地位较低人群的百分数。
- MEDV: 城镇住房价格中位数。 我们不会使用到全部的数据特征。这里，仅选取 CRIM, RM, LSTAT 三个特征用于线性回归模型训练。我们将这三个特征的数据单独拿出来，并且使用 describe() 方法查看其描述信息。 describe() 统计了每列数据的个数、最大值、最小值、平均数等信息。
features = df[["crim", "rm", "lstat"]]
features.describe()
同样，我们将目标值单独拿出来。训练一个机器学习预测模型时，我们通常会将数据集划分为 70% 和 30% 两部分。
其中，70% 的部分被称之为训练集，用于模型训练。例如，这里的线性回归，就是从训练集中找到最佳拟合参数
的值。另外的 30% 被称为测试集。对于测试集而言，首先我们知道它对应的真实目标值，然后可以给学习完成的模型输入测试集中的特征，得到预测目标值。最后，通过对比预测的目标值与真实目标值之间的差异，评估模型的预测性能。
上图就是一个简单的机器学习模型训练流程。接下来，我们针对数据集的特征和目标进行分割，分别得到 70% 的训练集和 30% 的测试集。其中，训练集特征、训练集目标、测试集特征和测试集目标分别定义为：X_train, y_train, X_test, y_test。
target = df["medv"] # 目标值数据
split_num = int(len(features) * 0.7) # 得到 70% 位置
X_train = features[:split_num] # 训练集特征
y_train = target[:split_num] # 训练集目标
X_test = features[split_num:] # 测试集特征
y_test = target[split_num:] # 测试集目标
X_train.shape, y_train.shape, X_test.shape, y_test.shape
2.9.2 构建和训练模型
划分完数据集之后，就可以构建并训练模型。同样，这里要用到 LinearRegression() 类。对于该类的参数就不再重复介绍了。
model = LinearRegression() # 建立模型
model.fit(X_train, y_train) # 训练模型
model.coef_, model.intercept_ # 输出训练后的模型参数和截距项
得到结果(array([ 0.69979497, 10.13564218, -0.20532653]), -38.00096988969018)。 这便是我们回归模型的拟合参数。 $$f = 0.6997*x_1 + 10.1356 * x_2 - 0.2053 * x_3 -38$$
其中，$$x_1$$，$$x_2$$,$$x_3$$分别对应数据集中crim,rm和lstat列，接下来向训练好的模型中输入测试机的特征得到预测值。
preds = model.predict(X_test) # 输入测试集特征进行预测
preds # 预测结果
array([17.77439141, 21.09512448, 27.63412265, 26.78577951, 25.38313368,
24.3286313 , 28.4257879 , 25.12834727, 16.82806601, 20.76498858,
52.3350748 , -0.18169806, 12.01475786, 7.87878077, 15.13155699,
32.93748235, 37.07872049, 29.50613719, 25.50800832, 12.35867972,
9.08901644, 47.08374238, 35.31759193, 33.3738765 , 38.34913316,
33.10414639, 91.3556125 , 35.11735022, 19.69326952, 18.49805269,
14.03767555, 20.9235166 , 20.41406182, 21.92218226, 15.20451678,
18.05362998, 21.26289453, 23.18192502, 15.87149504, 27.70381826,
27.65958772, 30.17151829, 27.04987446, 21.52730227, 37.82614512,
22.09872387, 34.71166346, 32.07959454, 29.45253042, 29.51137956,
41.49935191, 62.4121152 , 13.64508882, 24.71242033, 18.69151684,
37.4909413 , 54.05864658, 34.94758034, 15.01355249, 30.17849355,
32.22191275, 33.90252834, 33.02530285, 28.4416789 , 69.60201087,
34.7617152 , 31.65353442, 24.5644437 , 24.78130285, 24.00864792,
21.03315696, 27.84982052, 26.50972924, 48.2345499 , 25.50590175,
28.25547265, 28.66087656, 34.2545407 , 29.15996676, 27.8072316 ,
31.54282066, 32.22024557, 33.8708737 , 29.54354233, 24.7407235 ,
20.90593331, 31.85967562, 29.72491232, 25.59151894, 30.83279914,
25.40734645, 23.01153504, 27.01673798, 28.92672135, 27.49385728,
28.34125465, 31.52461119, 29.61897187, 25.83925513, 39.26663855,
33.00756176, 27.73720999, 21.93359421, 24.42469533, 27.95623349,
25.37499479, 29.91401113, 26.20027081, 27.81044317, 29.97326914,
27.7027324 , 19.68280094, 21.44673441, 21.56041782, 29.24007222,
26.02322353, 24.20402765, 25.31745183, 26.79101418, 33.60357546,
18.91793831, 23.98036109, 27.29202266, 21.15709214, 28.14694161,
32.47276562, 27.13611459, 32.81994315, 36.13809753, 20.23338607,
20.43084078, 26.37366467, 24.87561302, 22.88298598, 13.67619651,
12.08004137, 7.6709438 , 19.00432321, 19.97736929, 17.49844989,
19.46809982, 15.97963066, 12.49219926, 18.01764782, 20.51997661,
15.46843536, 20.30123637, 26.88163963, 22.19647509, 31.58974789,
29.60675772, 21.5321567 ])
对于回归预测结果，通常会有平均绝对误差、平均绝对百分比误差、均方误差等多个指标进行评价。这里，我们先介绍两个：
平均绝对误差（MAE）就是绝对误差的平均值，它的计算公式如下：
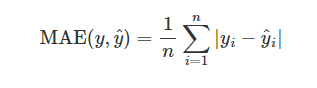
我们可以尝试用python实现MAE和MSE的计算函数：
def mae_solver(y_true: np.ndarray, y_pred: np.ndarray):
"""MAE 求解"""
n = len(y_true)
mae = sum(np.abs(y_true - y_pred)) / n
return mae
def mse_solver(y_true: np.ndarray, y_pred: np.ndarray):
"""MSE 求解"""
n = len(y_true)
mse = sum(np.square(y_true - y_pred)) / n
return mse
2.10 总结
我们从线性回归原理入手，学习了最小二乘法的两种求解方法，并针对线性回归算法进行了完整实现。在这个过程中，你了解到了机器学习的训练和预测流程，以及背后的数学思想。
总结而来，一个机器学习过程往往包含训练和预测两部分，训练好的模型可用于对未知数据的预测。而训练模型的过程，实际上是应用机器学习算法解决问题的过程。其中，我们通常会定义一个损失函数（平方损失函数），并使用一种数学优化方法（最小二乘法）去求解该损失函数的最优解。这个思想将始终贯穿于机器学习之中。